
안녕하세요
Bright_Ocean 입니다.
계란을 한바구니에 담지말라.. 투자계에서는 유명한 어구이지만
모든사람들의 투자 방법이 다 같지는 않습니다.
특정한 타점에 베팅하여 큰돈을 버는 사람도 있고
위험을 낮추어 천천히 오래가는 방법을 택하는 사람들도 있지요.
모두 내가 리스크를 어떤식으로 감당하느냐에 따라 달려있겠습니다.
각각의 개별주를 투자하는 것도 좋은 방법이지만
ETF를 통해 여러 주식을 한번에 사는 효과를 내는것도
투자에 좋은 방법이 될 수 있겠습니다.
그렇다면 ETF를 분산 투자할때는 어떤식으로 하는 것이 좋을까요?
분산투자의 원칙을 생각해본다면,
최악의 방법은 같은 방향으로 흐르는 ETF들을 모두 사는것이라 생각됩니다.
상승장에는 엄청난 수익을 가져다 줄 수 는 있겠으나,
하락장에는 또한 엄청난 손실을 감내해야 할 테니까요.
그래서 채권, 주식, 원자재 등의 ETF를 적절히 나누어 투자하는
올웨더 포트폴리오 같은 전략이 사람들의 입에 많이 오르내리는것 같습니다.
은퇴를 위한 소중한 내돈 한번의 하락장으로 모두 잃으면 눈물을 머금고
원금부터 다시 모아야 하니까요 ㅜㅜㅜ
오늘은 호주에서 10년이상 운용되고 있는 ETF들의 상관관계를 한번 찾아보았습니다.
investing.com에서 가격데이터는 추출하였습니다.
먼저 확인한 ETF들의 종류부터 살펴보실까요?
1. ETPMAG - ETFS Physical Silver
2. ETPMPD - ETFS Physical Palladium ETC
3. ETPMPT - ETFS Physical Platinum
4. ETPMPM - ETFS Physical Precious Metal Basket
5. IEM - iShares MSCI Emerging Markets
6. IEU - iSharesEurope
7. IJP - iShares MSCI Japan ETF (AU)
8. IKO - iShares MSCI South Korea ETF (AU)
9. IVE - iShares MSCI EAFE ETF (AU) (IVE)
10. IVV - iShares Core S&P 500 (IVV)
11. STW -SPDR S&P/ASX 200 Fund (STW)
investing에서 위의 11개의 가격데이터를 모두 다운받은뒤에 전부 파이썬으로 불러오기를 하였습니다
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
ETPMAG = pd.read_csv('ETPMAG.csv').sort_index(ascending = False)
ETPMAG.index = ETPMAG['Date']
ETPMAG = ETPMAG['Price']
가격데이터를 모두 파이썬에 올린뒤에
데이터를 모두 합쳐 하나의 데이터 프레임으로 만들어 주었습니다.
data = pd.concat([ETPMAG, ETPMPD, ETPMPT, ETPMPM, IEM, IEU, IJP, IKO, IVE, IVV, STW], axis = 1, join = 'inner')
data.columns = ['ETPMAG', 'ETPMPD', 'ETPMPT','ETPMPM', 'IEM', 'IEU', 'IJP', 'IKO', 'IVE', 'IVV', 'STW']
데이터 마다 시작되는 날짜가 다르기 때문에
가장 최근에 시작된 날짜고 inner merge 해주었더니
시작되는 날짜가 09년 4월부터가 되었네요.
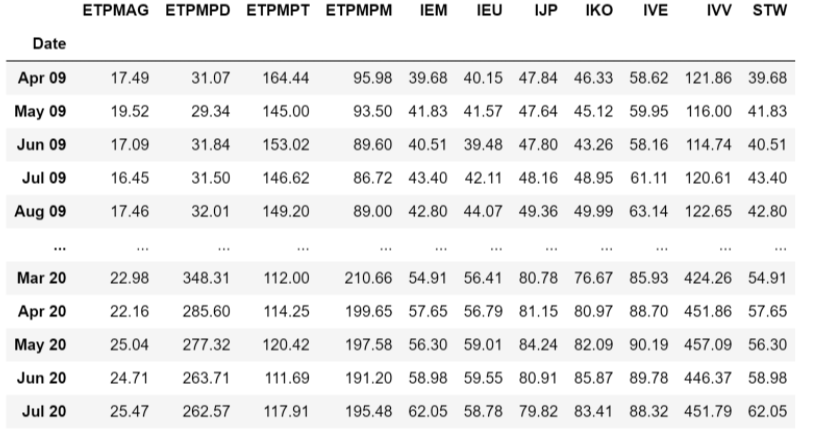
이제 상관계수를 한번 구해볼까요?
상관계수는 Heatmap으로 표현하면 아주 보기가 좋습니다.
import seaborn as sns
plt.figure(figsize = (8,8))
sns.heatmap(data.corr(), cmap ='coolwarm', annot =True, vmin = -1)
결과를 보시면,

위와 같게 나옵니다.
값이 0에 가까울 수록 상관성이 없음을 의미하며
1로 가까워 질수록(붉은색) 양의 상관관계
즉, 서로 같은방향으로 상승 또는 하락
-1로 가까워 질수록(파란색) 음의 상관관계
즉, 서로 다른 방향으로 상승 또는 하락
을 의미하게 됩니다.
결과를 살펴보자면 역시
주식으로 이루어져있는 IEM, IEU, IJP, IKO, IVE, IVV, STW는
서로 상관관계가 매우 높음을 알 수 있습니다.
이러한 ETF들을 여러개 산다면, 리스크 상으로는 좋지 못하다고 할 수 있겠지요
하락장에는 같이 떨어질 테니까요
신기한 점은 음의 상관관계가 높은 데이터도 보이는데 가장 높은 IVV(S&P500) 와 ETPMPT(Platinum)
의 가격데이터를 챠트로 나타내보면 아래와같이 음의 상관관계가 확실히 드러납니다.

그렇다면 서로 관련없는 즉 상관계수가 0에 가까운 두 데이터는 어떨까요?
가장 0 에 근접한 두 데이터는 -0.046을 나타내는 ETPMAG(은) 와 ETPMPD(팔라듐) 입니다.
아래와 같이 두 ETF의 가격 변동은 서로의 가격에 상관없이 즉 연관성이 없이 움직임을 알 수 있습니다.

이렇게 상관계수가 0에 가까운 ETF들을 나누어 담는것이 리스크 측면에서는 안전할 수 있겠지요.
정리해보자면,
1. 주식 데이터들을 가지는 ETF들은 서로 상관성이 높다.
2. 은과 팔라듐은 서로 상관성이 매우 낮았다.
3. 은은 주식시장의 가격들과 음의 상관성을 보이지만 높지는 않다.
결론적으로
(금은), (원자재), (주식시장)
에 분산 투자를 한다면 한가지 섹터에 몰빵하는 것보다는
리스크가 낮아질 수 있음을
데이터를 통해 확인하였습니다.
다음분석으로는
자산 배분을 실행하였을때 과연
어떤 이점이 있었는지 확인해보는 분석을 계획중에 있습니다.
그럼 다음에 만나요~
'경제적 독립하기 > [투자] Project tatabox' 카테고리의 다른 글
| [수익] 20.12.16 푸드웰 +297,409 (0) | 2020.12.28 |
|---|---|
| 6월 부터 12월까지의 투자정리 (2020 마무리) (0) | 2020.12.10 |
| 듀얼 모멘텀(VAA)전략을 이용한 호주 ETF 매수매도 백테스팅 해보기 (0) | 2020.07.10 |
| 호주 ASX 모든 주식 재무 데이터 자동으로 가져오기 (4) | 2020.07.05 |
| 계량투자를 위한 호주 주식 스크리닝 하기 (0) | 2020.07.01 |